字符串的相似度

1. 编辑距离（Edit Distance）
   • 将一个字符串转化成另一个字符串，需要的最少编辑次数（增加、删除、替换 一个字符）
   • 编辑距离越大，说明两个字符串的相似程度越小，对于两个完全相同的字符串，它们的编辑距离为 0
2. 编辑距离的常见计算方式
   • 莱文斯坦距离（Levenshtein Distance）
     • 允许 添加、删除、替换 字符
     • 表示两个字符串差异的大小
   • 最长公共子串长度（Longest Common Substring Length）
     • 允许 添加、删除 字符
     • 表示两个字符串相似程度的大小

计算莱文斯坦距离

1. 如果 a[i] == b[j]，则继续匹配 a[i+1] 和 b[j+1]

2. 如果 a[i] != b[j]

   • 删除 a[i]，匹配 a[i+1] 和 b[j]
   • 删除 b[j]，匹配 a[i] 和 b[j+1]
   • 在 a[i] 前添加一个和 b[j] 相同的字符，匹配 a[i] 和 b[j+1]
   • 在 b[j] 前添加一个和 a[i] 相同的字符，匹配 a[i+1] 和 b[j]
   • 将 a[i] 替换成 b[j]，或 b[j] 替换成 a[i] ，匹配 a[i+1] 和 b[j+1]

3. 状态转移方程法

   • 状态 （i，j）可以通过（i-1，j）、（i，j-1）、（i-1，j-1）三个状态中的任意一个转移过来
   • a[i] == b[j]，min_edist（i，j）=min（min_edist（i-1，j）+1，min_edist（i-1，j-1）+1，min_edist（i，j-1）+1）
   • a[i] != b[j]，min_edist（i，j）=min（min_edist（i-1，j）+1，min_edist（i-1，j-1），min_edist（i，j-1）+1）

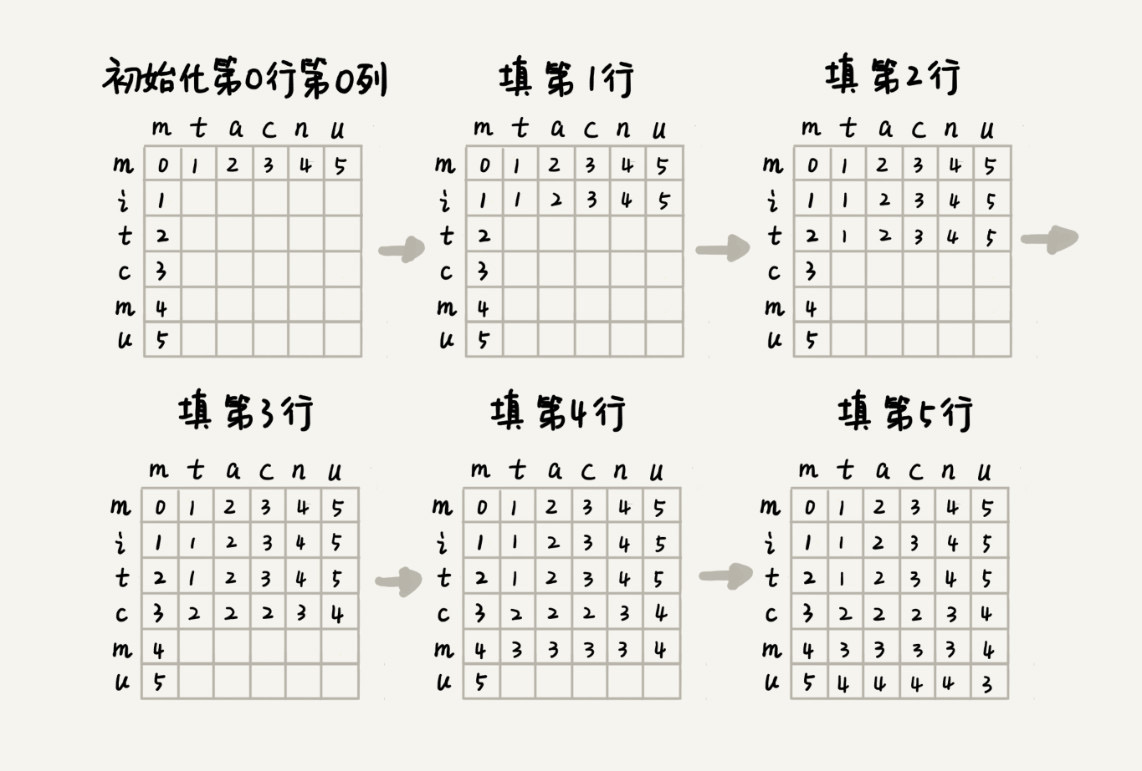
4. 状态转移表法

   

计算最长公共子串长度

1. 如果 a[i] == b[j]，则继续匹配 a[i+1] 和 b[j+1]
2. 如果 a[i] != b[j]
   • 删除 a[i]，匹配 a[i+1] 和 b[j]
   • 删除 b[j]，匹配 a[i] 和 b[j+1]
   • 在 a[i] 前添加一个和 b[j] 相同的字符，匹配 a[i] 和 b[j+1]
   • 在 b[j] 前添加一个和 a[i] 相同的字符，匹配 a[i+1] 和 b[j]
3. 状态转移方程法
   • 状态 （i，j）可以通过（i-1，j）、（i，j-1）、（i-1，j-1）三个状态中的任意一个转移过来
   • a[i] == b[j]，max_edist（i，j）=max（max_edist（i-1，j），max_edist（i-1，j-1）+1，max_max（i，j-1））
   • a[i] != b[j]，max_edist（i，j）=max（max_edist（i-1，j），max_edist（i-1，j-1），max_edist（i，j-1））

拼写纠错的优化

1. 取出编辑距离最小的 TOP 10，根据其他参数决策出选择哪个单词作为拼写纠错单词。如 根据搜索热门程度。
2. 使用多种编辑距离计算方法，分别求编辑距离最小的 TOP 10，然后求交集。
3. 统计用户的搜索日志，得到最常被拼错的单词列表，以及对应的拼写正确的单词。之后在拼写纠错时，先到这个单词列表中查找。
4. 针对每个用户都维护此用户的常用搜索关键词。当用户输入错误时，有现在常用的搜索关键词列表中计算编辑距离，查找编辑距离最小的单词。