图 Graph 相关概念

1. 顶点 Vertex：图中的元素
2. 边 Edge：图中的一个顶点与任意其他顶点建立的连接关系
3. 度 Degree：与顶点相连接的边的条数
4. 入度 In-degree：顶点的入度，表示有多少条边指向这个顶点
5. 出度 Out-degree：顶点的出度，表示有多少条边是以这个顶点为起点指向其他顶点
6. 有向图：图中的边带有方向
7. 无向图：图中的边不带有方向
8. 带权图：图中的每条边都有一个权重 weight

图的存储方式

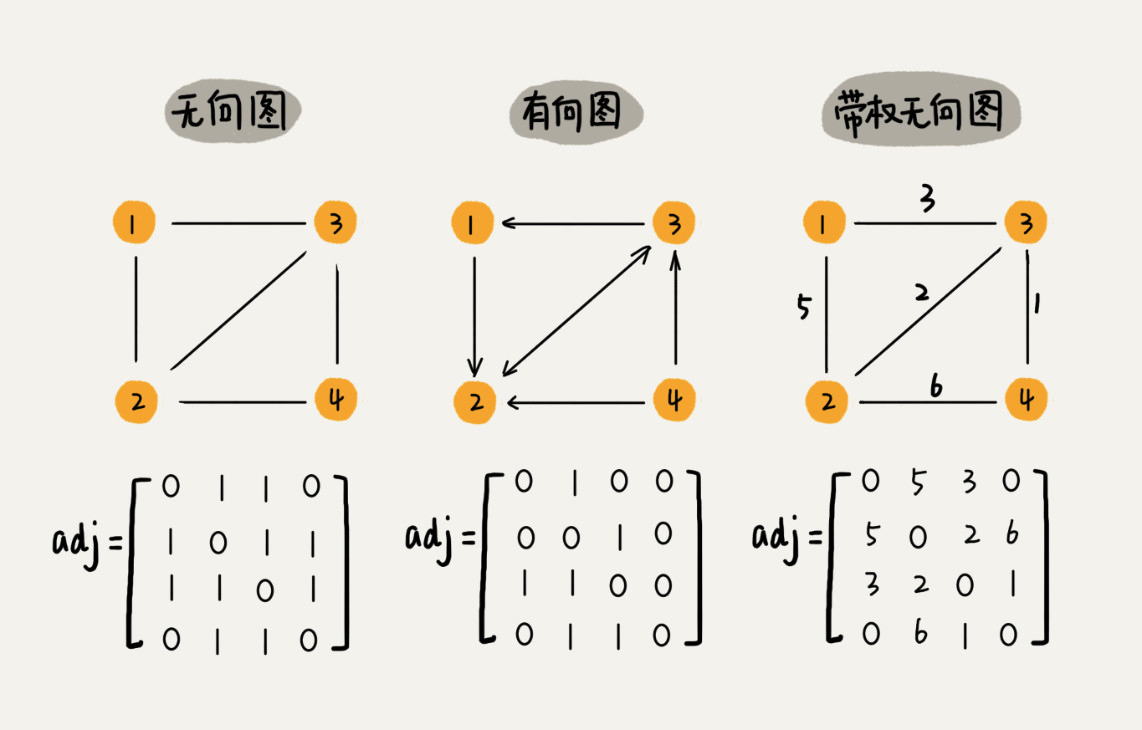
• 邻接矩阵 Adjacency Matrix

  

  1. 使用二维数组来存储
  2. 无向图 A
     • 如果顶点 i 与顶点 j 之间有边，就将 A[i][j] 和 A[j][i] 标记为1
     • 其余标记为 0
  3. 有向图 A
     • 如果顶点 i 与顶点 j 之间，有一条箭头从顶点 i 指向顶点 j 的边，就将 A[i][j] 标记为 1
     • 其余标记为 0
  4. 带权图
     • 在数组中存储相应的权重
  5. 优点：
     • 简单直观
     • 获取顶点的关系时，非常的高效
     3. 方便计算，可以将很多图的运算转换成矩阵之间的运算
  6. 缺点：比较浪费存储空间

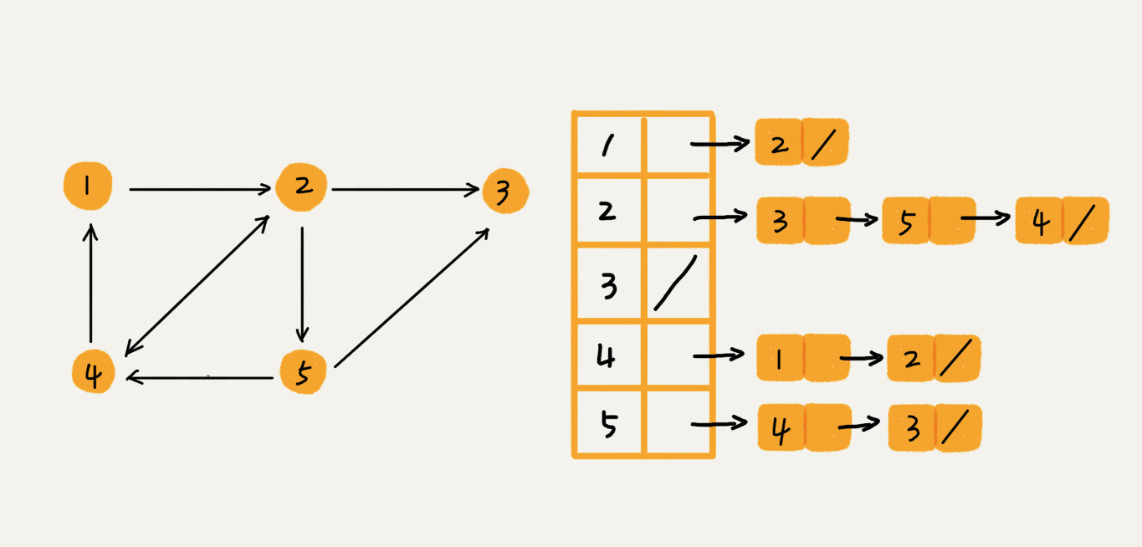
• 邻接表 Adjacency List

  

  1. 每个顶点对应一条链表，链表中存储的是与这个顶点相连接的其他顶点
  2. 链表的存储方式对缓存不太友好，可以将链表替换成其他更加高效的数据结构，如平衡二叉查找树、跳表、有序动态数组等
  3. 优点：比较节省存储空间
  4. 缺点：链表无法支持快速查找，可以使用跳表、红黑树、有序动态数组、散列表代替链表

图的应用

• 社交网络的好友关系

  1. 使用一个邻接表来存储好友关系的有向图，可以快速查找到某个用户关注了哪些用户，即此用户的关注列表
  2. 使用一个逆邻接表来存储好友关系，可以快速查找某个用户被哪些用户关注，即此用户的粉丝列表
  3. 使用链表的邻接表不能快速地判断两个用户之间的好友关系，可以将链表改为红黑树、跳表、有序动态数组、散列表中的一种
  4. 若是需要按照用户名称的首字母排序，分也来获取用户的粉丝列表或关注列表，则适合使用跳表。跳表的插入、删除、查找的时间复杂度为 O（logn），空间复杂度为 O（n），跳表本身的数据也是有序的。
  5. 如果数据太多，可以使用哈希算法等数据分片的方法，将邻接表存储在不同的机器上。或者利用外部存储，即数据库。