树 Tree 相关概念

1. 父节点、子节点、兄弟节点、根节点、叶子节点（叶节点）
2. 节点的高度（Height）
   • 节点到叶子节点的最长路径（边数），从最底层开始计数，计数的起点是 0
   • 树的高度 = 根节点的高度
3. 节点的深度（Depth）
   • 根节点到当前节点所经历的边的个数，从根节点开始度量，计数起点是 0
4. 节点的层数（Level）
   • 节点的深度 + 1

B+ 树 B+ Tree

1. B+ 树 是通过 B 树（二叉查找树）演化而来，目的是在二叉查找树中能够按照区间来查找数据
2. B+ 树中的非叶子节点不存储数据，只存储索引，而 B 树中的节点存储数据
3. B+ 树中的叶子节点使用链表串联起来，链表中的数据是有序的，可以按区间查找，而 B 树中的叶子节点不需要链表串联
4. B+ 树的根节点一般放在内存中，其他节点存储在磁盘中
5. B+ 树中的每个节点中子节点的个数不能超过 m 个，即 m叉树，也不能小于 m/2（除根节点外）

B+ 树的实现

1. B+ 树的非叶子节点存储索引，存储在磁盘中
   • 内存的访问速度是纳米级别的，磁盘的访问速度是毫秒级别的，读取同样大小的数据，从磁盘中读取花费的时间是从内存中读取的上万倍，甚至几十万倍
   • 每个节点的读取操作，都对应一次磁盘 IO 操作
   • 树的高度 = 每次查询数据时磁盘 IO 操作的最大次数
   • 尽量减少磁盘 IO 操作，也就是尽量降低树的高度
2. B+ 树的叶子节点存储的是 k 个数据行的键值、地址信息、当前节点在链表中的前驱节点的地址、当前节点在链表中的后继节点的地址，k 的取值由事先计算得到
3. B+ 树是一个 m 叉树，m 的取值由事先计算得到
4. k、m 的计算方式
   • 操作系统按照页（PAGE_SIZE）的方式读取内存、磁盘中的数据，一页的大小通常为 4KB，可以通过 getconf PAGE_SIZE 命令查看
   • 当读取的数据量超过一页时，会触发多次 IO 操作
   • k、m 的取值则根据每个节点的大小 <= 页的大小，且尽可能的大

B+ 树的操作

1. 查询

   • 按照主键的值在树中进行查找，当查找到叶子节点后
     • 若查找主键 ，则根据叶子节点中的地址信息，获取到具体数据
     • 若查找范围区间，则在链表中继续查找，直到不满足条件（达到 limit 限制、超过范围区间），获取到符合区间值的所有数据

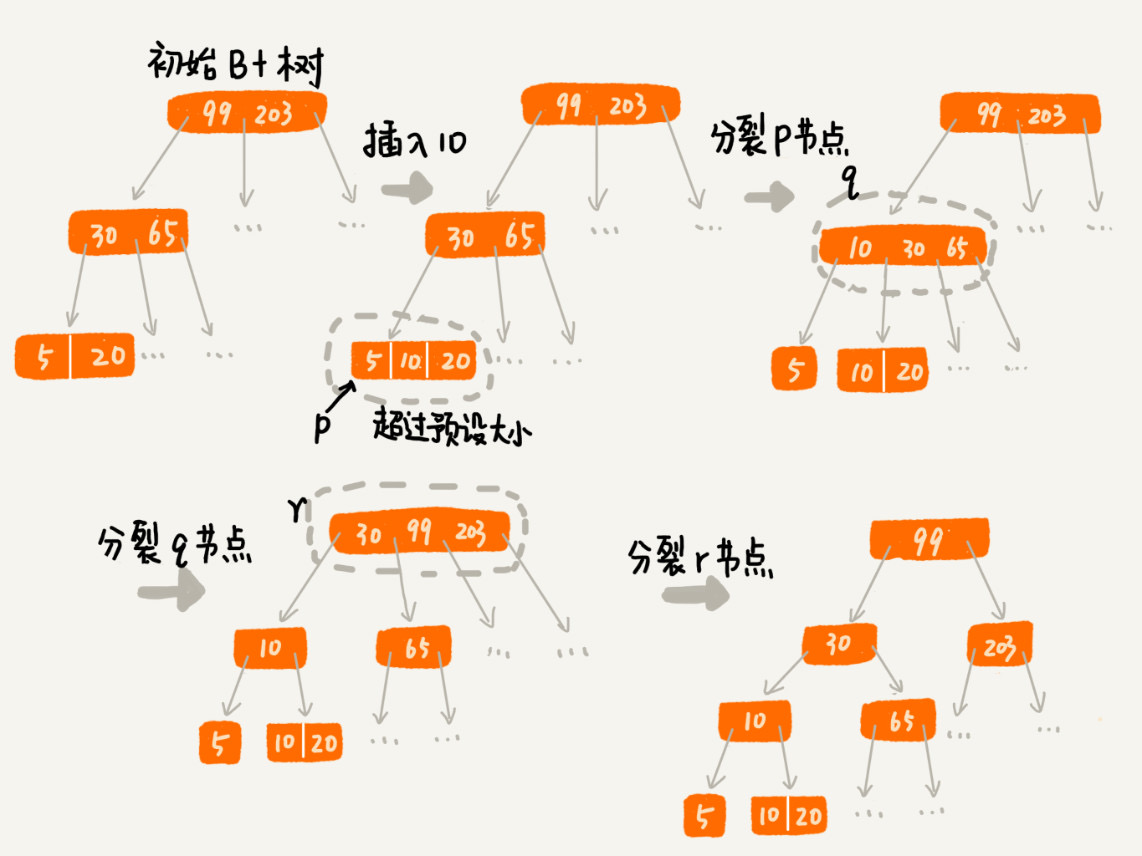
2. 插入

   • B+ 树中，m 值是由事先计算得出，即每个节点最多只能有 m 个子节点
   • 当插入数据时同时更新索引，插入后的节点个数超过 m 个，则需要对索引进行更新分裂操作
   • 将当前节点分裂成两个节点，若当前节点分裂之后，父节点的子节点个数超过 m 个，则继续向上分裂，直至父节点的子节点个数 < m

   

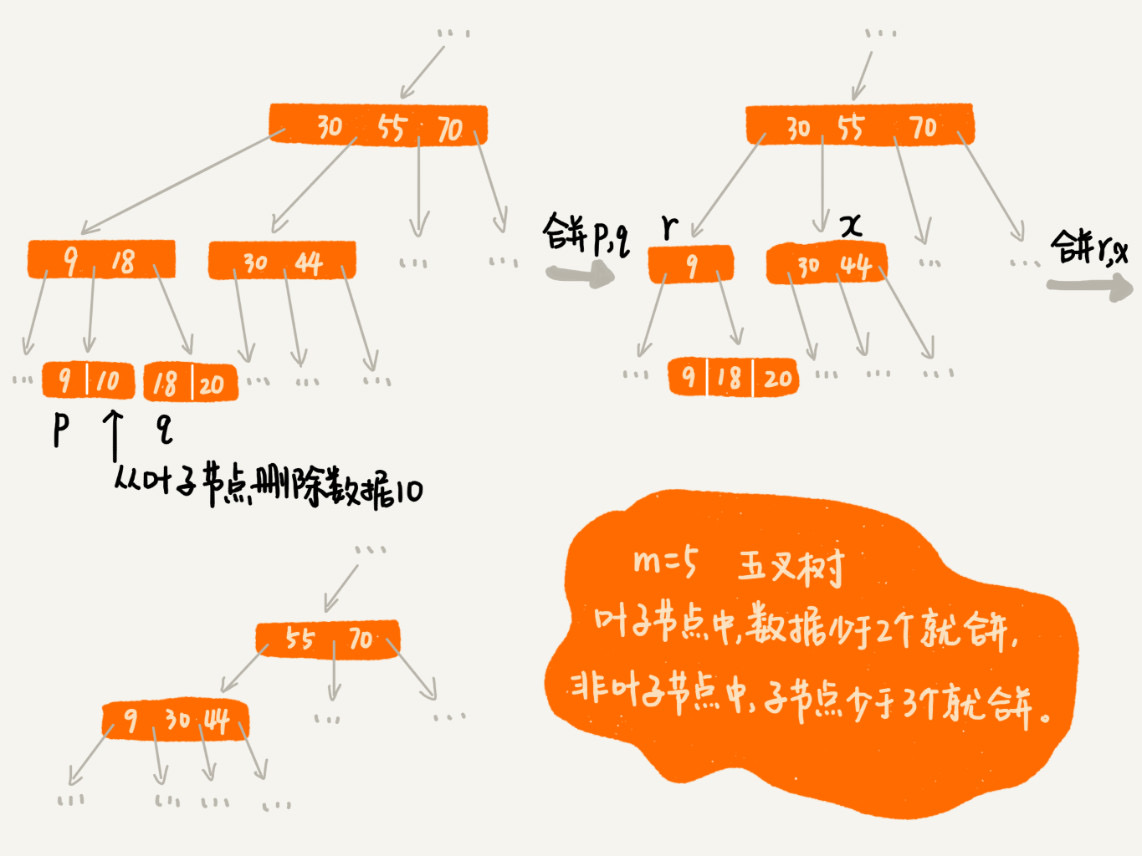
3. 删除

   • 删除某个数据同时删除索引，当删除后的节点个数小于 m/2 时，则需要对索引进行更新合并操作
   • 当前节点的个数小于 m/2，将当前节点和它相邻的兄弟节点合并
   • 若合并之后的节点个数超过 m，则执行插入的“分裂”操作