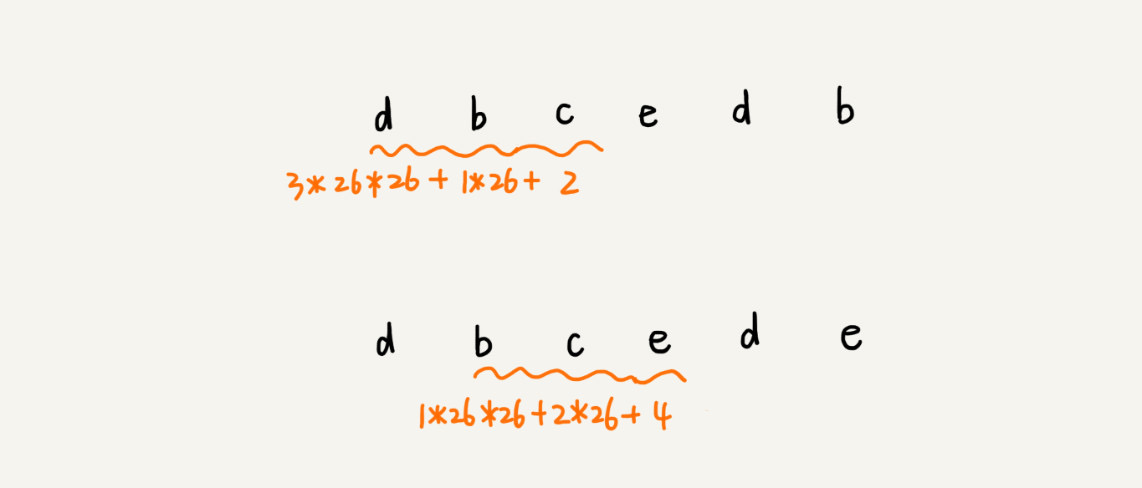Brute Force 暴力匹配算法/朴素匹配算法

1. 思想
   • 在主串中，匹配模式串。若主串的长度是 n，模式串的长度是 m，则 n >= m。主串可以按照模式串的长度 m，得出 n - m + 1 个子串。
   • 将主串中起始位置为 0，长度为 m 的子串 x，与模式串的每一位字符依次比较。若相等则继续，不相等则进行下一步。
   • 若不匹配，则将主串中的起始位置加 1。循坏执行上一步，直到主串的起始位置大于 n - m + 1 或 匹配成功。
2. 时间复杂度：O（n*m）
3. 优点
   • 思路简单，代码易实现，维护简单，是最常见的处理小规模的字符串匹配算法
   • 在实际应用中，时间复杂度往往远低于 O（n*m）

Rabin-Karp

1. 思想
   • 在 BF 算法上进行优化，利用哈希算法减少匹配时的时间复杂度，但是匹配的次数没有减少。
   • 将主串中得出的 n - m + 1 个子串分别求哈希值。依次和模式串的哈希值比较。
   • 有技巧地计算子串的哈希值

     • 假设要匹配的字符串的字符集中包含 k 个字符，使用 k 进制来表示一个子串。

     • 将代表子串的 k 进制数字转换成十进制。

     • 在相邻的两个子串的哈希值计算公式存在以下关系：

       

       • B = （A - 第一位的 k 进制值） * k + 最后一位的 k 进制值
       • 第一位的 k 进制 = （km-1）* 此字符表示的 k 进制的数字
       • km 可以提前算好存储在数组中，下标为 m 的值为 km
   • 若可能存在哈希冲突，则将哈希值相等的子串和模式串再一次进行比较
2. 时间复杂度：O（n），当可能存在大量的哈希冲突时，则退化为 O（n*m）
3. 缺点
   • 可能会有散列冲突

Boyer-Moore BM 算法

1. 目的
   • 尽可能地一次性跳过多个字符，从后往前的比较字符，用来减少 BF（暴力匹配）算法的匹配次数，以提升算法的效率
2. 思想

   • 坏字符规则

     

     • 从后往前的将模式串和主串进行匹配
     • 找到主串“坏字符”对应下标
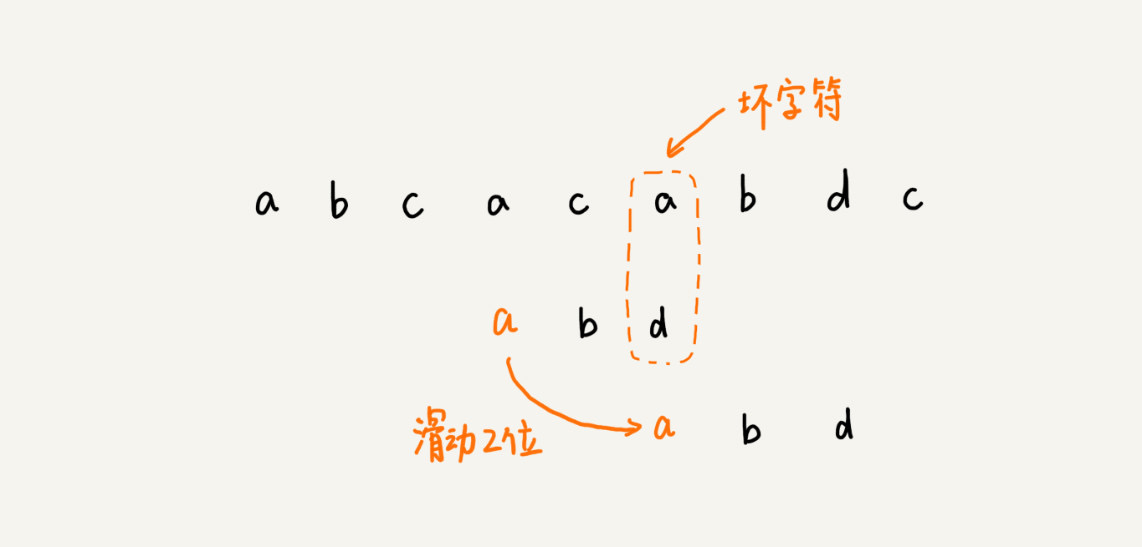
       • 若存在不匹配的字符，将主串中对应的字符标记为“坏字符”，并记录“坏字符”的位置为 si
     • 找到模式串中另一个与主串中“坏字符”相等的字符
       • 在模式串中查找是否存在另一个与主串中的“坏字符”相等的字符
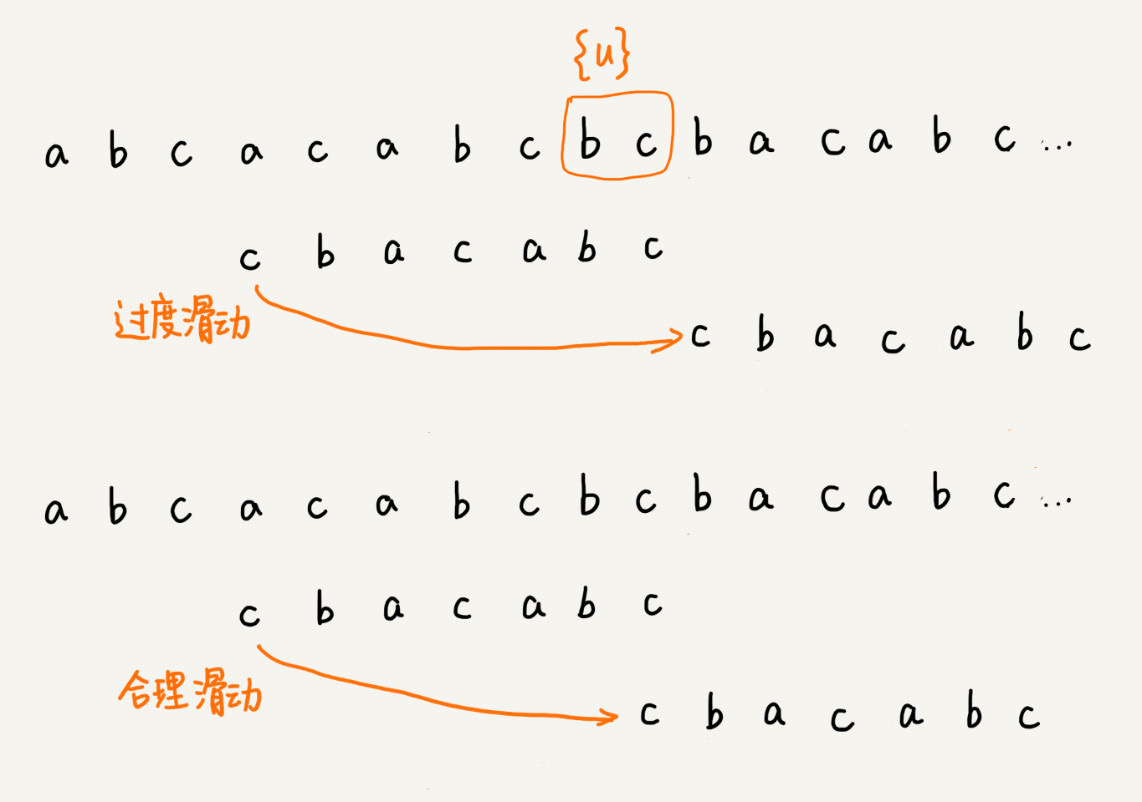
       • 若模式串中存在一个或多个与主串中“坏字符”相等的字符，则记录下最后出现的位置为 xi（以免跳过太多字符，导致错过可以正确匹配的字符），跳过 si - xi 个字符
       • 若不存在，则直接跳过模式串长度个字符
     • 注意事项
       • si - xi 有可能出现负数的情况
       • 例如：主串为 aaaaaa，模式串为 baa，当比较模式串中的 b 时，主串中“坏字符”的位置为 0，模式串中的位置为 2（取最后一个），则跳过字符的个数为 0 - 2 = -2
       • 为了避免出现跳跃负数个字符，还需要“好后缀规则”

   • 好后缀规则

     • 从后往前的匹配模式串和主串

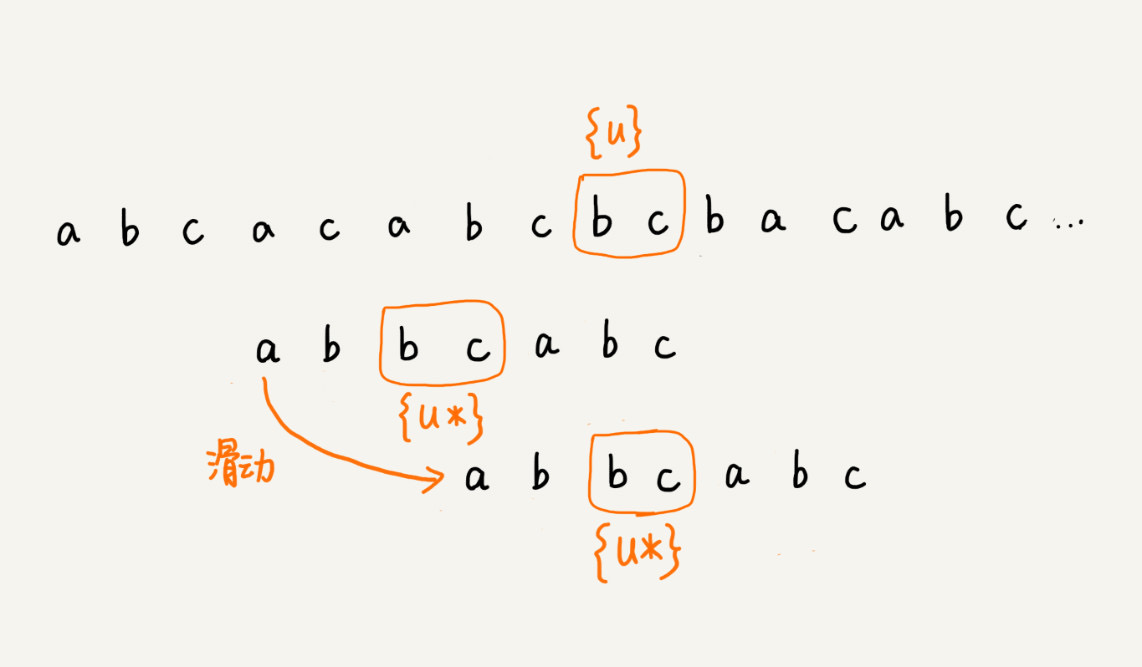
     • 找到主串中的“好后缀”{u}

       • 某个不匹配字符之后的字符串，就是“好后缀”{u}

     • 找到模式串中另一个与主串中“好后缀”相等的字符串

       • 在模式串中查找是否存在与主串中“好后缀”相等的字符串

       • 如果存在一个或多个与主串中“好后缀”相等的字符串，则找到最后一个相等的字符串 {u*}，将 {u*} 跳跃对应到 {u} 的位置

         

       • 如果模式串中不存在与“好后缀”相等的字符串，则需要判断匹配到的好后缀中，在模式串中是否存在相等的前缀子串

       • 如果模式串中存在后缀子串和前缀子串相等的字符串，则跳跃到前缀子串最长能匹配到的位置

       • 如果模式串中不存在后缀子串和前缀子串相等的字符串，则跳跃模式串长度个字符

         

     • 注意事项

       • 当坏字符规则和好后缀规则同时存在时，可判断这两种情况下得出的跳跃字符个数，选择较大的跳过。可以避免坏字符规则出现负数的情况。
       • 当内存条件受限时，可只采用好后缀规则。
3. 应用
   • 文本中的查找功能
   • linux grep 的功能

BM 算法的代码分析

• 坏字符规则
  • 需要找到“坏字符”在模式串中最后出现的位置，即 xi
    1. 每次将“坏字符”在模式串中进行顺序查找（效率太低）
    2. 使用散列表存储模式串每个字符出现的最后位置，可以使用数组或者对象，默认值是 -1，即在模式串中没有此字符
• 好后缀规则

  1. 需要找到“好后缀”在模式串中，除本身外最后出现的位置

     • 使用 suffix 数组，数组的下标表示“好后缀”的长度，数组中的值表示除本身外最后出现的位置

       

  2. 需要找到与模式串的前缀子串与模式串后缀子串重合的位置

     • 使用 prefix 数组，数组的下标表示后缀子串的长度，数组中的值表示是否存在后缀子串与前缀子串相等的字符串

       

  3. 如果 suffix 对应后缀子串长度的值不为 -1，则表示模式串中存在（除本身之外）与“好后缀”相等的字符串，则将模式串中最后出现的“好后缀”字符串对应到主串中的“好后缀”字符串

     • 若主串中“坏字符”位置为 j，模式串的长度为 m
     • 主串中“好后缀”字符串的起始位置为 j + 1，“好后缀”长度为 k，k = m - j - 1
     • 需要移动的位数为：j + 1 - suffix[k]

  4. 如果 suffix 对应后缀子串长度的值为 -1，即模式串中不存在（除本身之外）与“好后缀”相等的字符串，则判断 prefix 数组中，下标为 [ 0～好后缀长度 ] 的值

     • 倒序查找下标为 [ 0～好后缀长度 ]，找到符合条件最长的前缀子串
     • 如果 prefix 对应后缀子串长度的值为 false，则表示模式串的前缀子串不存在和后缀子串重合的字符串，则移动的位数为：模式串的长度 m
     • 如果 prefix 对应后缀子串长度的值为 true，即模式串的前缀子串存在和后缀子串重合的字符串，则移动的位数为：模式串的长度 m - prefix 的下标

  5. 如何填充 suffix 和 prefix 数组

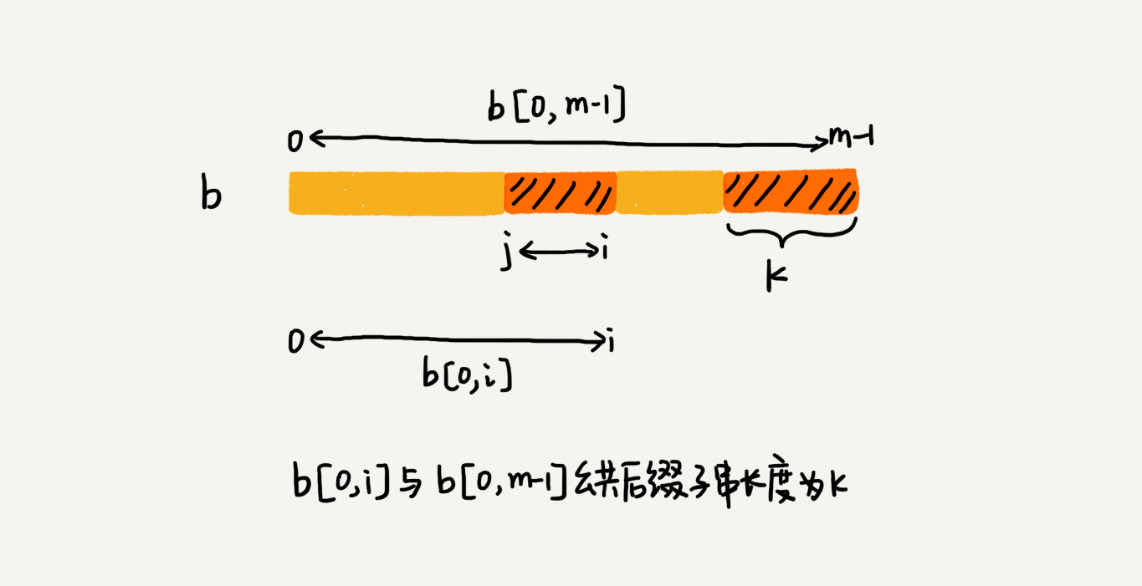
     • 模式串的长度为 m，则模式串为 B [ 0，m - 1 ]
     • 将 B [ 0，m - 1 ] 分别与 B [ 0，i ] 求公共后缀子串，i 的取值为 0 ～ m - 2
       • 如果公共后缀子串的长度为 k，则 suffix[k] = j，j 表示公共后缀子串的起始位置
       • 如果 j = 0，则表示模式串的后缀子串和前缀子串有重合，prefix[k] = true

     

参考资料

http://www.cs.jhu.edu/~langmea/resources/lecture_notes/boyer_moore.pdf

Knuth Morris Pratt KMP 算法

1. 目的

   • 尽可能地一次性跳过多个字符，从前往后的比较字符，用来减少 BF（暴力匹配）算法的匹配次数，以提升算法的效率
   2. 在已经匹配的前缀子串 A 中，看看 A 的后缀子串有没有和 A 的前缀子串重合，如果有的话，重合的部分可以不用比较

2. 思想

   • 从前往后的将模式串与主串进行匹配
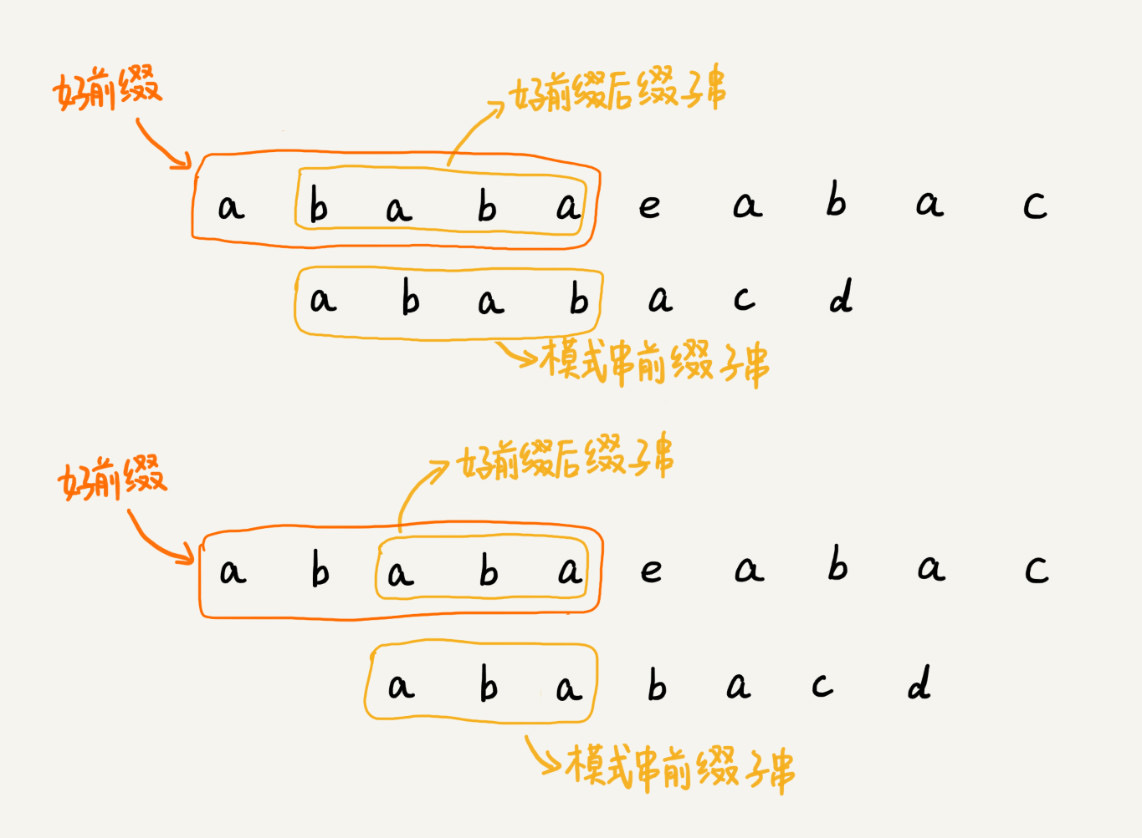
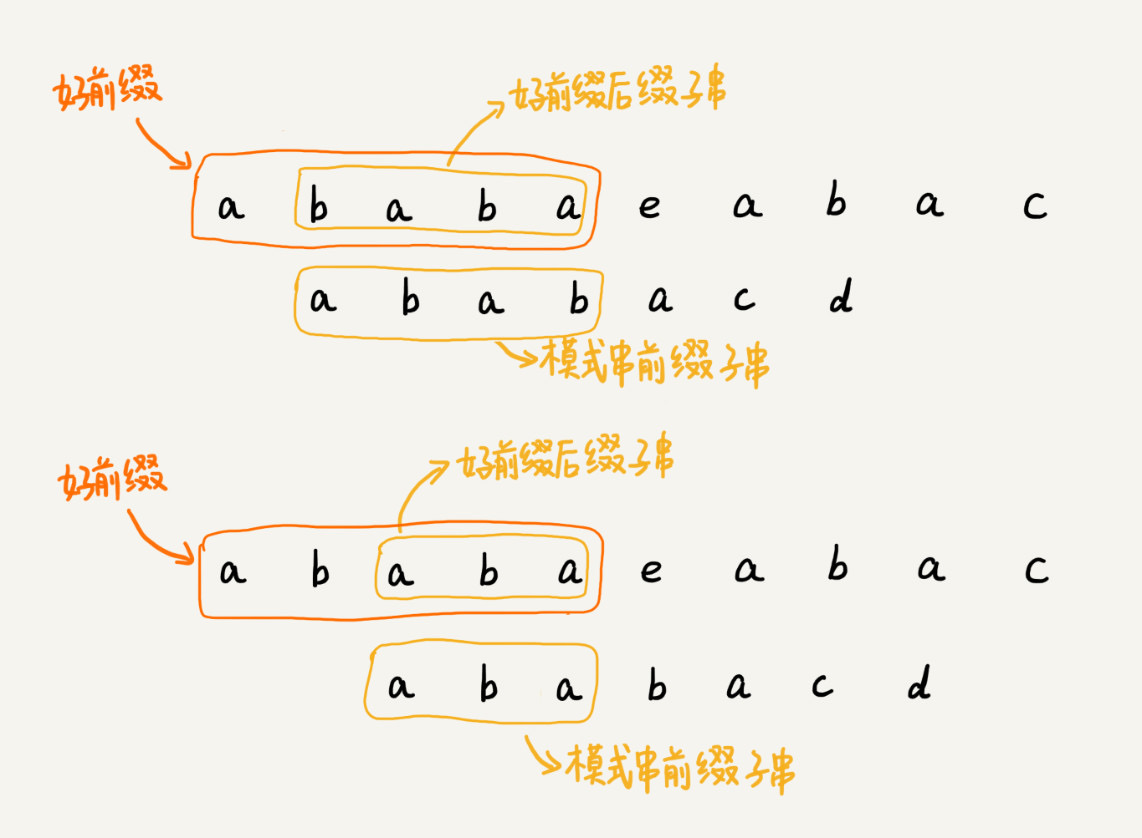
   • 当出现不能匹配的“坏字符”时，将之前可以匹配到的字符串称为“好前缀”
   • 如果“好前缀”中的后缀子串和模式串的前缀子串有重合，则可以跳过重合的部分，继续依次比较后面的字符。将“好前缀”后缀子串中最长可匹配模式串的前缀子串，称为“最长可匹配后缀子串”，对应的前缀子串称为“最长可匹配前缀子串”

   

   

KMP 算法的代码分析

1. 求模式串中前缀子串的“最长可匹配前缀子串”

   • 使用 next 数组（失效函数），数组的下标代表模式串的前缀子串的长度，数组中的值为这个前缀子串对应的“最长可匹配前缀子串”的结尾字符下标（或这个前缀子串的“最长可匹配前缀子串”的长度 - 1）

     

   • 利用动态规划来求 next 数组

     • 若 next[i - 1] = k - 1，即 B[0，i - 1] 对应的“最长可匹配好前缀”为 B[0，k - 1]
     • 当 B[i] == B[k] 时，则 next[i] = next[i - 1] + 1，即 next[i] = k
     • 当 B[i] != B[k] 时
       • 假设 B[i - 1] 存在一个“可匹配好后缀”（不是“最长可匹配好后缀”）为 B[x，i - 1]，则对应的“可匹配前缀子串”为 B[0，i - 1 - x]。如果 B[i] == B[i - x]，则说明 B[x，i] 是 B[0，i] 的“最长可匹配后缀子串”
       • 如果不存在 B[i] == B[i - x]，则说明 next[i] = -1，即不存在“最长可匹配前缀子串”

2. 将模式串与主串依次匹配，当出现“坏字符”时，获取对应“好前缀”的 next 数组（失效函数）的值 n，主串的匹配位置不变，将模式串移动 n 位，继续匹配

Trie 树（字典树）

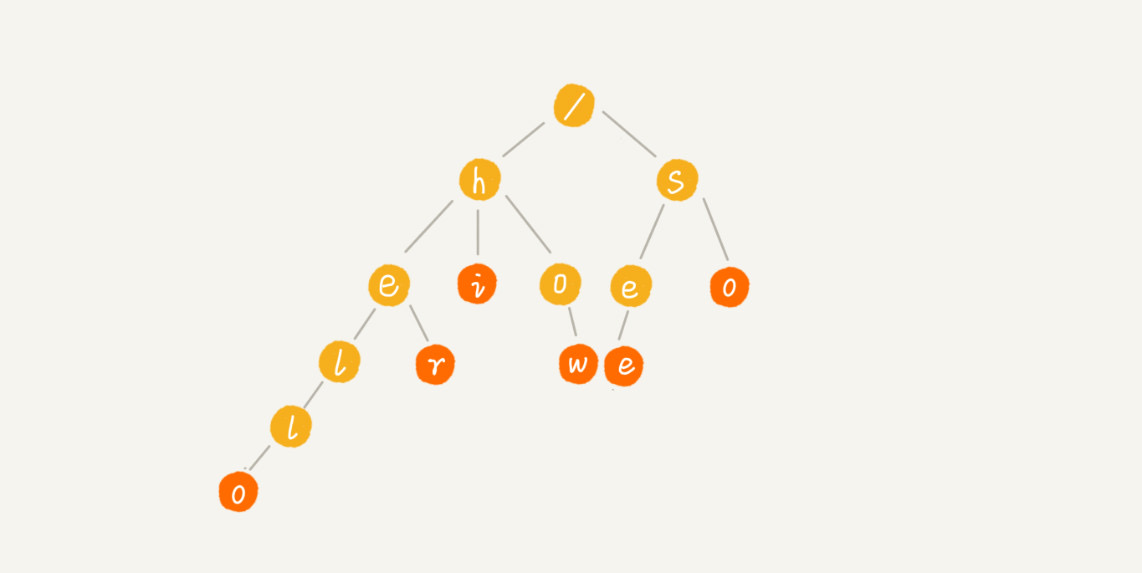
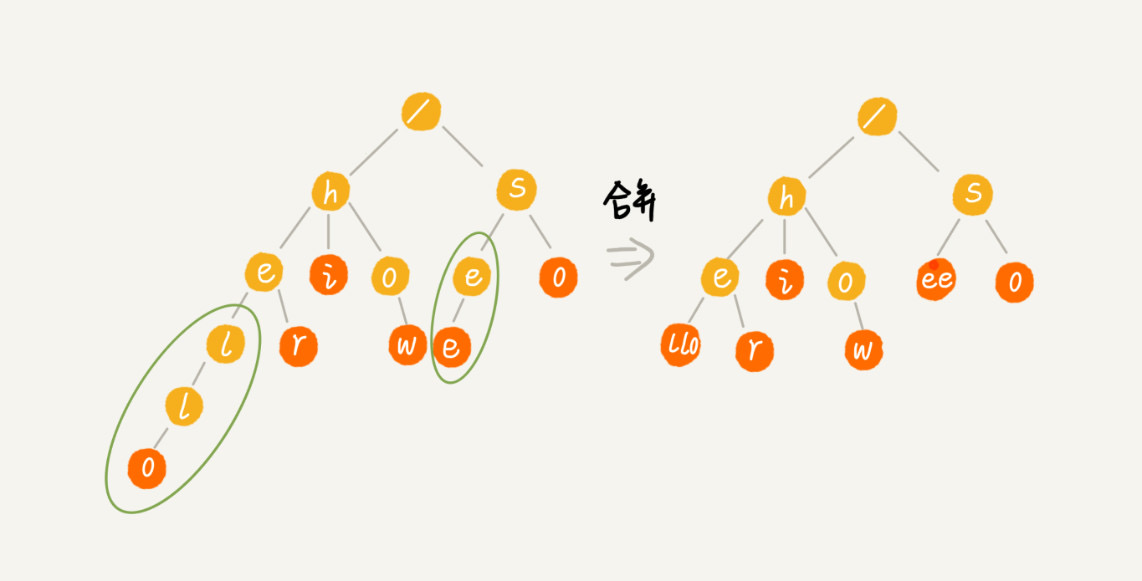
1. 一组字符串复用公共前缀后，所构成的树形结构，当单个字符串结束时，需要将节点标识为结束（下图中的红色节点）

   

2. 适用场景

   • 在确定的一组字符集中，频繁查找或匹配不同的字符串，如 关键字检测
   • 在确定的一组字符集中，查找或匹配符合前缀的字符串，如 搜索框自动补全

3. 字符集要求

   • 字符集中，字符串的公共前缀重合较多

Trie 树 的操作

1. 构建 Trie 树
   • 根结点不存放任何字符，仅作为开始节点
   • 根据字符集中的字符串，存储为多叉树，相同公共前缀的字符串拥有相同的父节点
     • 存储为多叉树的方法有很多，如 有序数组、跳表、红黑树等
   • 将字符串的最后一个字符，标识为结束节点，结束节点可以是叶子结点，也可以是任意一个父节点
2. 在 Trie 树中查找字符串
   • 当要查找的字符串的最后一个字符在 Trie 树中标识为结束节点时，则匹配成功，否则为匹配失败

Trie 树的优缺点

1. 优点
   • 在已确定的字符集中，且字符集中的字符串的公共前缀较多。适合频繁的查找能否匹配成功，复杂度为 O（k），k 为要查找的字符串的长度
   • 适合查找前缀匹配的字符串
2. 缺点
   • 每个节点需要维护子节点的指针，数据块不连续，对缓存不友好，内存消耗大
   • 改进 Trie 树，使其内存消耗减少时，效率降低，且编码难度增大，不如直接使用红黑树
     • 如 缩点优化

       

AC 自动机（Aho-Corasick）

1. 适用场景
   • 适用于于多模式串匹配，即在一个主串中查找多个模式串
2. 目的
   • 类似于 KMP 算法，尽可能地一次性跳过多个字符，用于减少匹配次数
   • 一次性地寻找多个模式串
3. AC 自动机的本质就是在 Trie 树上添加类似 KMP 的 next 数组，只不过 AC 自动机的 next 数组是构建在 Trie 树上

AC 自动机的操作

1. 构建 Trie 树

   • 根结点不存放任何字符，仅作为开始节点
   • 根据字符集中的字符串，存储为多叉树，相同公共前缀的字符串拥有相同的父节点
     • 存储为多叉树的方法有很多，如 有序数组、跳表、红黑树等
   • 将字符串的最后一个字符，标识为结束节点，结束节点可以是叶子结点，也可以是任意一个父节点
   • 在结束节点上记录模式串的长度，匹配时使用

2. 在 Trie 树上构建失败指针

   • 失败指针的意义

     • 输入的字符与当前结点的所有孩子结点都不匹配时，AC 自动机的状态应该转移到的状态
     • 从根结点到当前结点所组成的字符串 与 整个 Trie 树 中的所有前缀 的最长公共部分

   • 根结点的失败指针为 NULL，指向自己，按层遍历整个 Trie 树

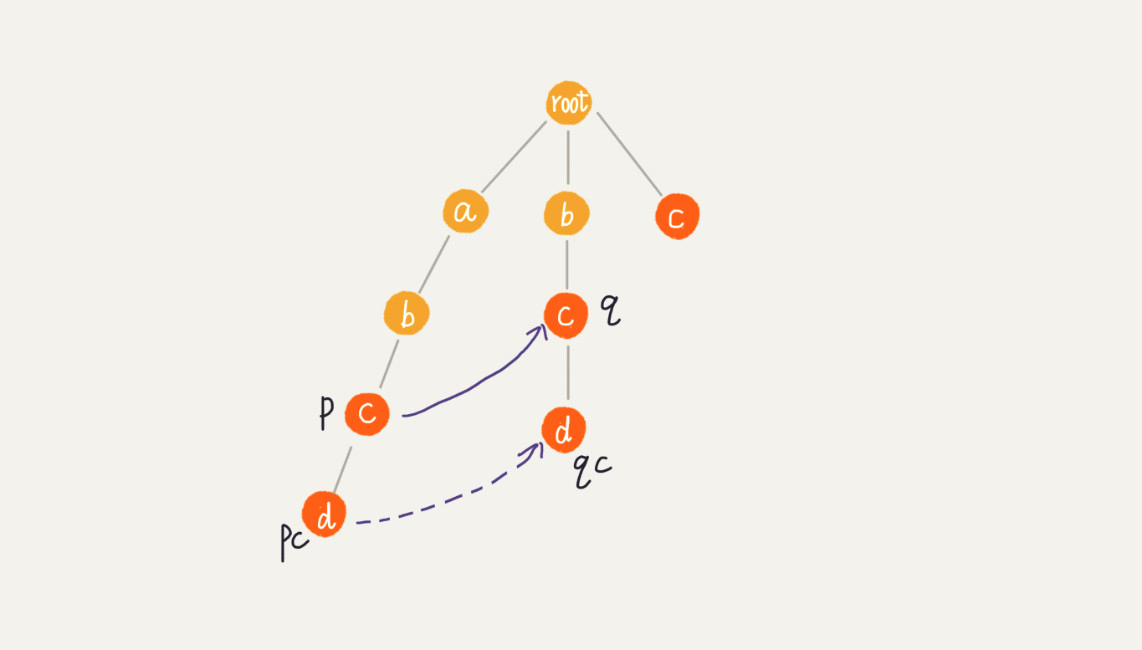
   • 如果当前结点对应的字符和当前结点父节点指向的失败指针的孩子结点对应的字符一致，则当前结点的失败指针指向当前结点父节点的失败指针的孩子结点

     • p.fail == q && pc == qc，则 pc.fail = qc

     

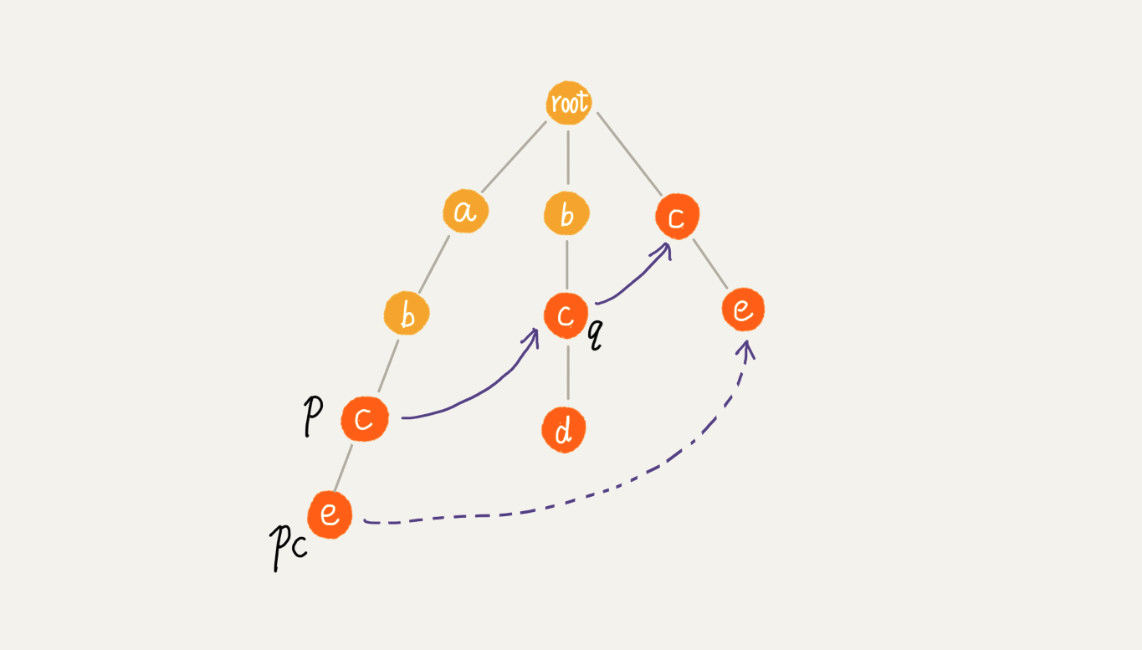
   • 如果当前结点对应的字符和当前结点父节点指向的失败指针的孩子结点对应的字符不一致，比较当前结点对应的字符和父节点的失败指针的失败指针，直到找到失败指针的孩子结点对应的字符与之相等，如果不存在，则当前结点的失败指针指向根结点

     • p.fail = q && pc != q.children，则令 q = q.fail，继续比较

     

3. 在 AC 自动机中匹配主串

   • 当前结点的指针从根结点开始，主串字符从 0 开始匹配
   • 匹配当前结点的孩子结点和当前主串字符
     • 如果相等，则判断当前结点和当前结点的失败指针指向的结点，是否是字符串的结束字符
       • 如果是，将匹配到的字符保存在结果集中
       • 如果不是，当前结点指向孩子结点，继续匹配主串字符
     • 如果不相等，则判断当前结点的失败指针是否指向 NULL
       • 如果是，则令当前结点的指针指向根结点，继续匹配主串字符
       • 如果不是，则令当前结点的指针指向当前结点失败指针的结点，继续匹配失败指针的孩子结点和当前主串字符