树 Tree 相关概念

1. 父节点、子节点、兄弟节点、根节点、叶子节点（叶节点）
2. 节点的高度（Height）
   • 节点到叶子节点的最长路径（边数），从最底层开始计数，计数的起点是 0
   • 树的高度 = 根节点的高度
3. 节点的深度（Depth）
   • 根节点到当前节点所经历的边的个数，从根节点开始度量，计数起点是 0
4. 节点的层数（Level）
   • 节点的深度 + 1

二叉树 Binary Tree

二叉树

1. 每个节点最多有两个子节点，分别是左子节点和右子节点
2. 满二叉树
   • 叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点
   • 满二叉树的高度大约是 log2(n)
3. 完全二叉树
   • 叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大
   • 完全二叉树的高度是 log2(n) 向下取整
4. 存储二叉树
   • 基于指针或引用的二叉链式存储法
     • 每个节点有三个字段，分别存储数据、左右子节点的指针
   • 基于数组的顺序存储法
     • 根节点存储在下标为 1 的位置
     • 若节点存储在数组中下标为 i 的位置，左子节点存储在下标 2 * i 的位置，右子节点存储在下标 2 * i + 1 的位置
5. 遍历二叉树
   • 前序遍历
     • 对于树中的任意节点，先打印这个节点，再打印它的左子树，最后打印它的右子树
   • 中序遍历
     • 对于树中的任意节点，先打印它的左子树，再打印它本身，最后打印它的右子树
   • 后序遍历
     • 对于树中的任意节点，先打印它的左子树，再打印它的右子树，最后打印它本身
   • 递归公式
     • 前序遍历的递推公式：preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
     • 中序遍历的递推公式：inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
     • 后序遍历的递推公式：postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r

二叉查找树 / 二叉搜索树（Binary Search Tree）

1. 前提是一颗完全二叉树 ，在树中的任意一个节点，其左子树中的每个节点的值，都小于这个节点的值，而右子树节点的值都大于这个节点的值
2. 查找操作
   • 先取根节点，如果等于要查找的数据，则返回，若查找的数据比根节点的值小，则在左子树中递归查找，若查找的数据比根节点的值大，则在右子树中递归查找
3. 插入操作
   • 如果要插入的数据比节点的数据大
     • 节点的右子树为空，直接将新数据插入到右子节点的位置
     • 节点的右子树不为空，继续递归遍历右子树
   • 如果要插入的数据比节点的数据小
     • 节点的左子树为空，直接将新数据插入到左子节点的位置
     • 节点的左子树不为空，继续递归遍历左子树
4. 删除操作
   • 如果要删除的节点没有子节点
     • 直接将父节点中指向要删除节点的指针置为 null
   • 如果要删除的节点只有一个子节点（左子节点或右子节点）
     • 更新父节点中指向要删除节点的指针，让它指向要删除节点的子节点
   • 如果要删除的节点有两个子节点
     • 找到这个节点的右子树中的最小节点，替换到要删除的节点上，删除这个最小节点
     • 或者找到这个节点的左子树中的最大节点，替换到要删除的节点上
5. 取巧的删除操作
   • 单纯地将要删除的节点标记为“已删除”，没有真正地从树中将这个节点去掉，比较浪费内存空间
6. 快速地查找最大节点和最小节点、前驱节点和后继节点
7. 中序遍历二叉查找树，可以输出有序的数据序列，时间复杂度是 O(n)
8. 时间复杂度跟树的高度成正比，也就是 O(height)

支持重复数据的二叉查找树

1. 二叉查找树中的每个节点不仅仅存储一个数据，通过链表和支持动态扩容的数据等数据结构，把值相同的数据都存储在同一个节点上
2. 二叉查找树中的每个节点只存储一个数据，插入相同值时，将要插入的数据放到这个节点的右子树，把这个新插入的数据当作是大于这个节点的值来处理

二叉查找树的优势（与散列表相比）

1. 散列表中的数据是无序存储的，而二叉查找树的中序遍历可以在 O（n）的时间复杂度内，输入有序的数据
2. 散列表扩容耗时多，而且遇到散列冲突时性能不稳定，平衡二叉查找树的性能稳定，时间复杂度为 O（logn）
3. 由于哈希冲突，散列表的查找速度不一定比平衡二叉查找树的效率高
4. 散列表的构造复杂，需要考虑到散列函数的设计、冲突解决办法、扩容、缩容等，而平衡二叉查找树只需要考虑平衡性的问题
5. 为了避免过多的散列冲突，散列表装载因子不能过大，会浪费一定的存储空间

递归树

递归的思想是，将大问题分解为小问题来求解，然后再将小问题分解为小小问题。这样一层一层地分解，直到问题的数据规模被分解得足够小，不用继续递归分解为止。如果把这个一层一层的分解过程画成图，它其实就是一棵树，这棵树就是递归树。

借助递归树分析递归算法的时间复杂度

• 分析快速排序的时间复杂度

  

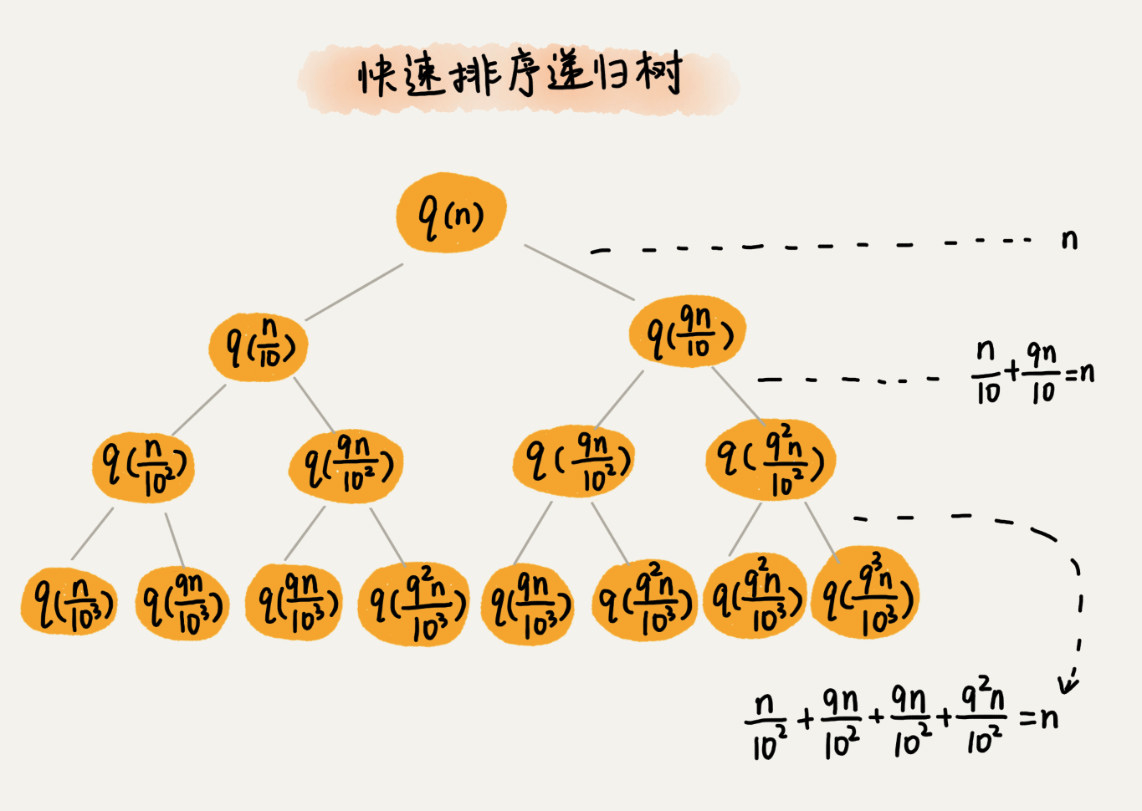
  • 假设每次分区后，两个分区的大小比例为 1 ： k，递推公式可以写成 T（n）= T（n / 10）+ T（9n / 10）
  • 每层分区操作所遍历的个数之和是 n（固定）
  • 当分区不能均匀的一分为二时，递归树不是满二叉树，那么递归树的高度介于最短路径（每次都是 1 / 10）和最长路径（每次都是 9 / 10）之间，所以时间复杂度介于 nlog10（n）和 nlog9/10（n）之间，时间复杂度仍然是 O（nlog（n））

• 分析斐波那契数列的时间复杂度

  

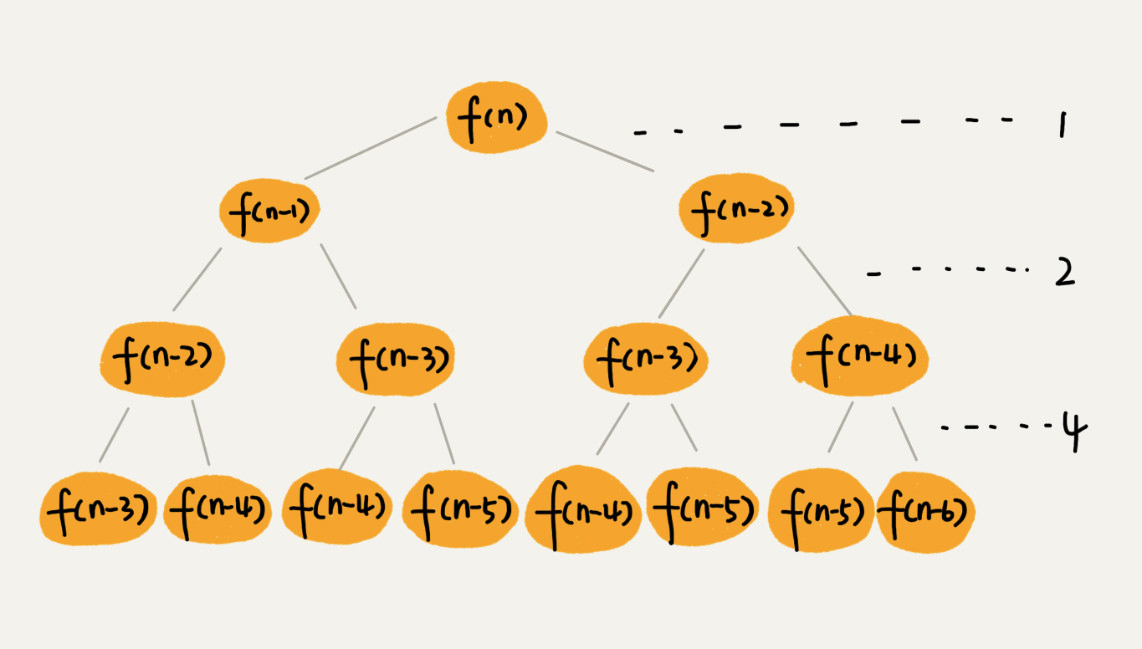
  • f（n） = f（n - 1） + f（n - 2），每次数据规模都是 -1 或者 -2，叶子结点的数据规模是 1 或者 2。
  • 最长路径是 n（每次走 1 的数据），最短路径是 n / 2（每次走 2 的数据）
  • 合并操作需要一次加法运算，第一层的时间消耗是 1，第二层是 2，第三层是 4。如果是最长路径，则总时间消耗是 1 + 2 + 4 + … + 2n + 1。如果是最短路径，则总消耗时间是 1 + 2 + … + 2n/2 + 1。
  • 时间复杂度介于 O（2n）和 O（2n/2）之间

• 分析全排列的时间复杂度

  • 把 n 个数据的所有排列都找出来，如果确定了最后一位数据，就变成了求解剩下 n - 1 个数据的排列问题。所以 n 个数据的排列问题，可以分解成 n 个 n - 1 个数据的排列的子问题。
  • f(1,2,…n) = {最后一位是1, f(n-1)} + {最后一位是2, f(n-1)} +…+{最后一位是n, f(n-1)}。