应用背景
- 广度、深度优先搜索,都是应用于图的搜索算法,是一种暴力搜索的算法。
- 其他应用于图的搜索算法
- A*
- IDA*
广度优先搜索 BFS(Breadth First Search)
- 主要目的:在图中寻找两个顶点间的路径
- 思想:
- 类似于“地毯式搜索”,主要包含两个步骤
- 不断地访问顶点
- 将“路径”记录下来
- 访问顶点
- 将顶点的相邻顶点放入队列中,作为下一个需要访问的顶点。
- 如果此顶点已经被访问过,则继续下一个访问下一个需要访问的顶点。
- 记录“路径”
- “路径”,即将每个顶点作为相邻顶点的“上一步”记录下来
- 最终的路径为从终点开始,依次根据“上一步”找到起点
- 当找到终点时停止访问顶点
- 类似于“地毯式搜索”,主要包含两个步骤
- 代码实现要点
- visited 数组:记录顶点是否被访问
- queue 数组:记录需要被访问的顶点
- prev 数组:记录相邻顶点的“上一步”为访问顶点
- 复杂度分析
- 时间复杂度
- 每个顶点最多被访问一次,每个边也最多被访问一次
- O(V+E),V 为顶点的个数,E 为边的个数
- 在连通图中,E 一定会大于等于 V - 1
- O(E)
- 空间复杂度
- 使用邻接表记录顶点的相邻顶点
- O(V)
- 时间复杂度
深度优先搜索 DFS(Depth First Search)
- 主要目的:在图中寻找两个顶点间的路径
- 思想:
- 回漱思想,类似于“走迷宫”,当发现“无路可走”时,返回上一个“岔路口”,主要包含两个步骤
- 不断地访问顶点
- 将“路径”记录下来
- 访问顶点
- 不断地“深入”访问相邻顶点,直到顶点无相邻顶点或者顶点的相邻顶点已经被访问过
- 当找到终点时停止访问顶点
- 记录“路径”
- “路径”,即将每个顶点作为相邻顶点的“上一步”记录下来
- 最终的路径为从终点开始,依次根据“上一步”找到起点
- 回漱思想,类似于“走迷宫”,当发现“无路可走”时,返回上一个“岔路口”,主要包含两个步骤
- 代码实现要点
- 使用递归来实现
- visited 数组:记录顶点是否被访问
- prev 数组:记录相邻顶点的“上一步”为访问顶点
- found 布尔值:记录是否找到终点
- 复杂度分析
- 时间复杂度 O(E)
- 每个顶点最多被访问两次,每个边最多被访问两次
- 空间复杂度 O(V)
- 时间复杂度 O(E)
双向广度优先搜索
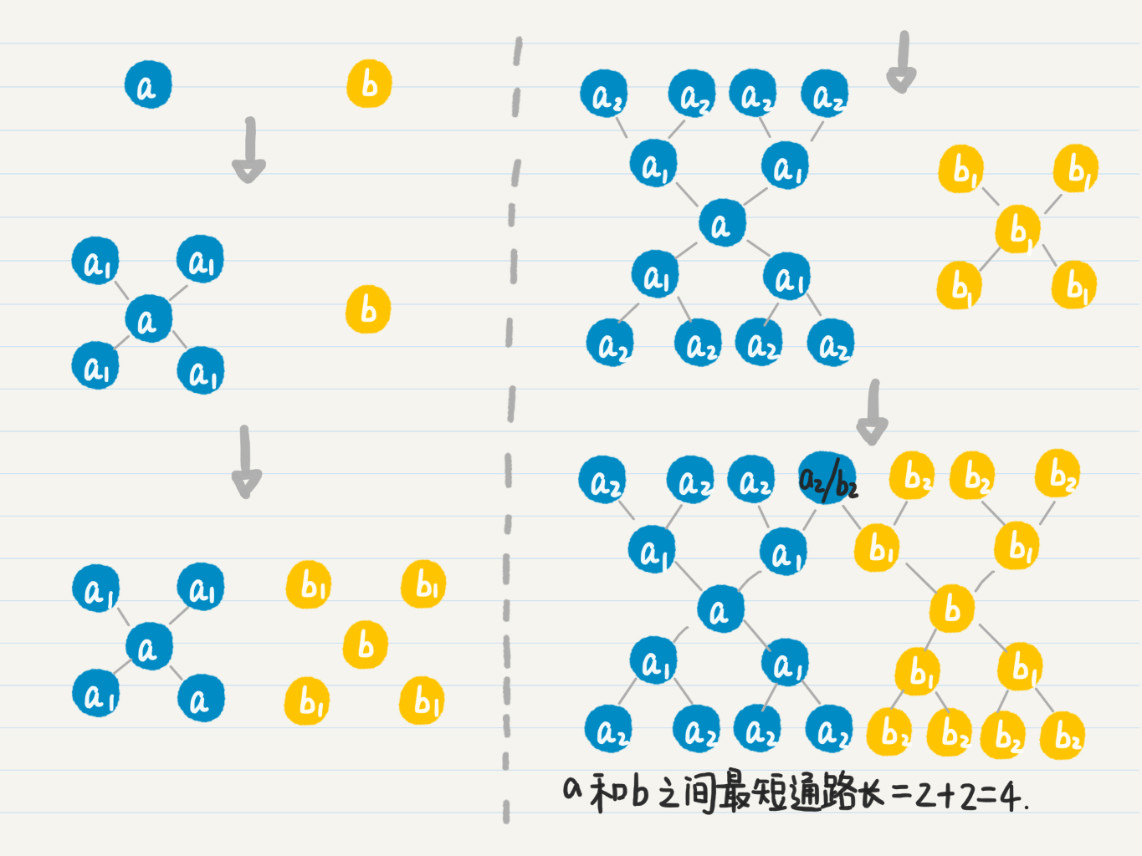
求两个结点 a、b 的最短路径
- 从 a 出发,进行广度搜索,记录下 a 的所有一度结点 a1,查看 b 是否出现在集合 a1 中,如果有,则停止
- 从 b 出发,进行广度搜索,记录下 b 的所有一度结点 b1,查看 a、a1 是否出现在 b 和 b1 的并集中
- 重复上述两步,直到找到 a 和 b 的好友的交集 c,则 a、b 的最短通路长为 a 到 c 的通路长度 + b 到 c 的通路长度
启发式搜索算法 Heuristically Search Algorithm
- A* 搜索算法属于启发式搜索算法(Heuristically Search Algorithm),是对 Dijkstra 算法的优化和改造
- 启发式搜索算法利用估价函数,避免“跑偏”,贪心地朝着最有可能到达终点的方向前进。启发式搜索算法找出的路径不一定是最短路径,但可以更加快速地找到最短路线
A* 搜索算法 A Star Search Algorithm
- 遍历顶点时,从起点到这个顶点的路径及路径的长度是确定的,记作 g(i),i 表示顶点编号
- 通过启发函数(Heuristic Function),即使用一个估算值来判断从这个顶点到终点的路径长度,避免“跑偏”,记作 h(i)
- 可以使用这个顶点到终点之间的直线距离,即欧几里得距离,近似地估计路径长度
- 欧几里得距离涉及到比较耗时的开根号计算,可以使用更加简洁的曼哈顿距离(Manhattan Distance),只有简单的加减计算
- 使用估价函数(Evaluation Function),来综合判断该优先遍历哪个顶点,记作 f(i)。譬如 f(i)= g(i)+ h(i)
A* 搜索算法和 Dijkstra 算法的区别
- 优先级队列构建的方式不同
- A* 搜索算法是根据估价函数(f(i))来构建优先级队列
- Dijkstra 算法是根据从起点到当前顶点的路径长度(g(i))来构建优先级队列
- A* 搜索算法在更新顶点的路径长度(g(i))时,也会同步更新估价函数的值(f(i))
- 循环结束的条件不同
- A* 搜索算法遍历到终点时就结束
- Dijkstra 算法在终点出优先级队列时结束
- A* 搜索算法找到的路径不是最短路径,Dijkstra 算法找到的路径是最短路径